Kolmogorov-Smirnov Test

Population: $Y\sim$ some population distribution with c.d.f $F$

Sample: n i.i.d from population, $Y_1,\dots ,Y_n$

Parameter: Whole CDF

Null hypothesis: $H_0:F=F_0$, versus $H_A:F\ne F_0$

Kolmogorov-Smirnov Test

Test statistic

$$D\left(F_0\right)=\underset{y}{sup}\left|\hat{F}\left(y\right)-F_0\left(y\right)\right|$$

where $\hat{F}\left(y\right)$ is the empirical cumulative distribution function:

$$\hat{F}\left(y\right)=\frac{1}{n}\sum _{i=1}^{n}11\left\{Y_i\le y\right\}$$

and $F_0$ is the cumulative distribution function for the null hypothesized distribution.

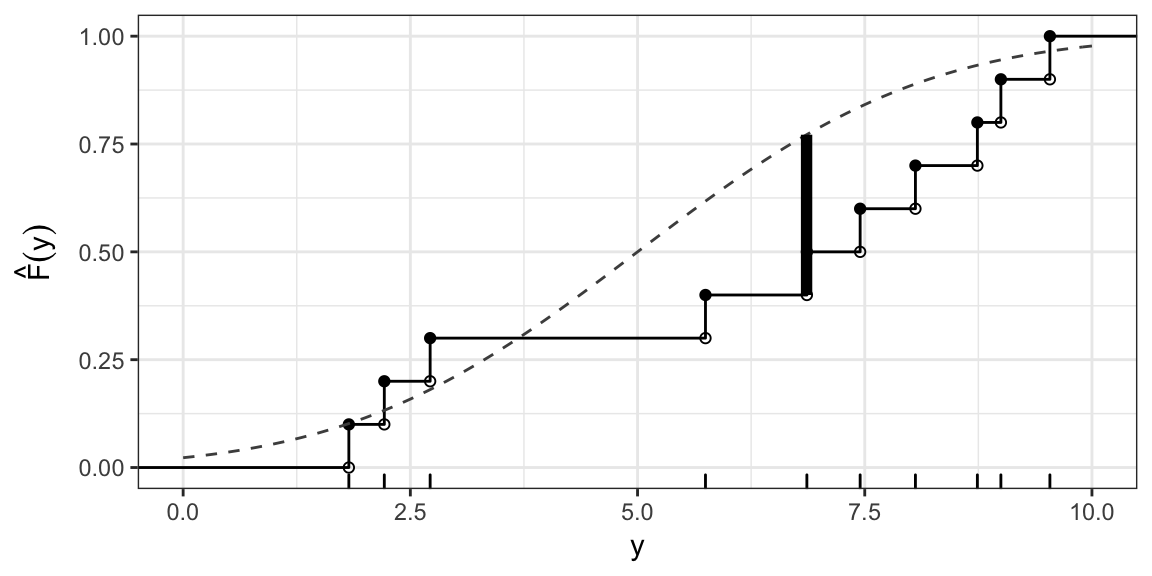
ECDF: Example

Sample values: 1.8, 2.2, 2.7, 5.7, 6.9, 7.4, 8.1, 8.7, 9 and 9.5

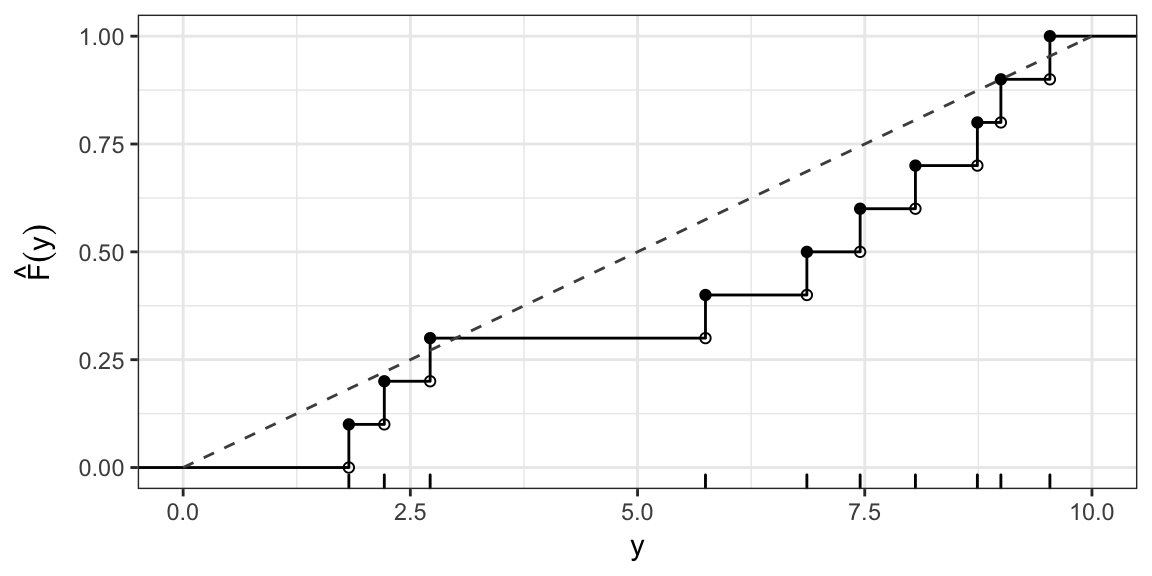
KS test statistic: Uniform(0, 10)

Say, $$H_0:F\left(Y\right)=\{\begin{array}{cc}0,& y\le 0\\ \frac{y}{10},& 0<y\le 10\\ 1,& y>10\end{array}$$

I.e. $H_0:Y\sim \text{Uniform}(0,10)$

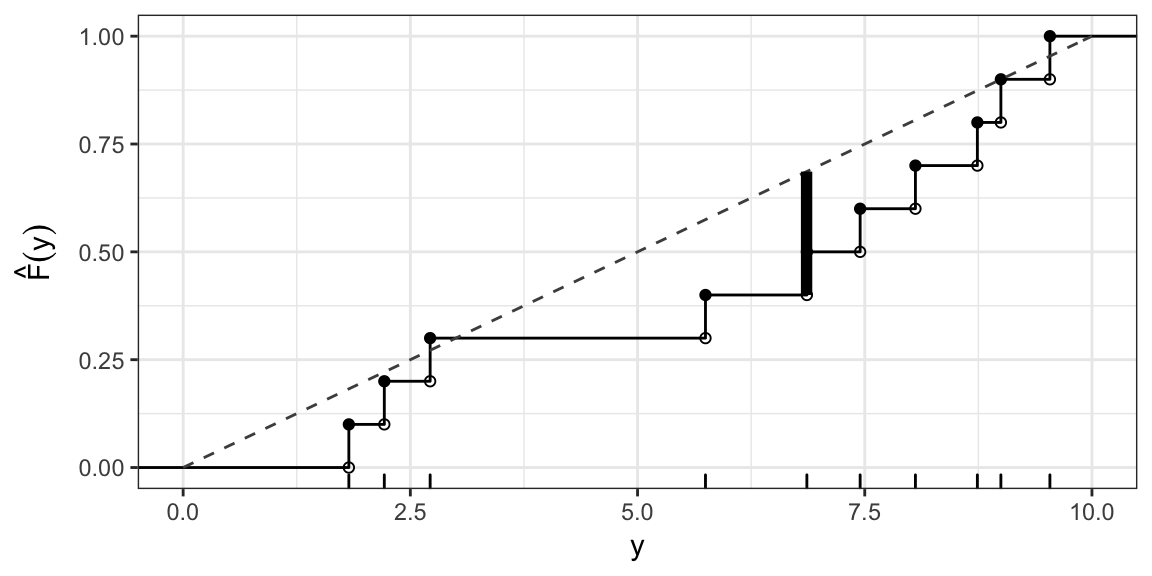
KS test statistic: Uniform(0, 10) cont.

$D\left(F_0\right)={sup}_y\left|\hat{F}\left(y\right)-F_0\left(y\right)\right|\approx 0.29$ (occurs at $y$ just less than 6.9)

KS test statistic: Normal(5, 6.25)

$H_0:Y\sim \text{Normal}(5,6.25)$

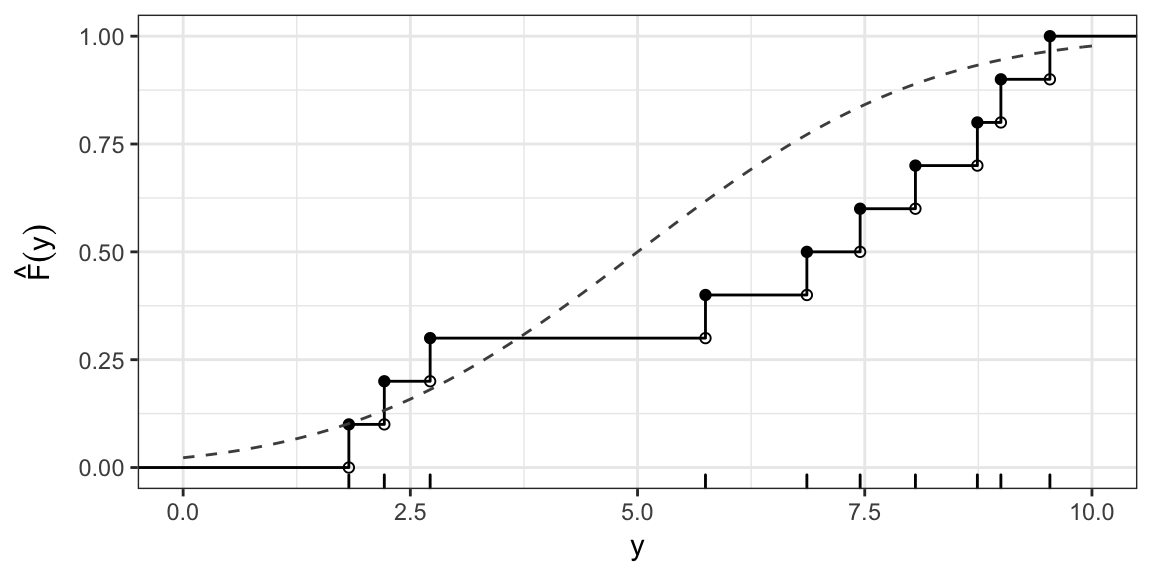
KS test statistic: Example cont.

$D\left(F_0\right)={sup}_y\left|\hat{F}\left(y\right)-F_0\left(y\right)\right|\approx 0.37$ (occurs at $y$ just less than 6.9)

Reference Distribution?

$$\sqrt{n}D\left(F_0\right){\to }_{d}K$$ where $K$ is the Kolmogorov Distribution.

Reject $H_0$ for large values of $\sqrt{n}D\left(F_0\right)$.

In R

ks.test(x = y, y = punif, min = 0, max = 10)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  y
## D = 0.28632, p-value = 0.3209
## alternative hypothesis: two-sided

One sided tests

Lesser alternative: $$H_A:F<F_0,\text{i.e.}F\left(y\right)<F_0\left(y\right)\text{for all}y$$

Test statistic $$D^{-}\left(H_0\right)=\underset{y}{sup}\left(F_0\right(y)-\hat{F}(y\left)\right)$$

Greater alternative: $$H_A:F>F_0,\text{i.e.}F\left(y\right)>F_0\left(y\right)\text{for all}y$$

Test statistic $$D^{+}\left(H_0\right)=\underset{y}{sup}\left(\hat{F}\right(y)-F_0(y\left)\right)$$

One sided tests are hard to interpret

Example based on simulated data. $H_0:Y\sim N(0,100)$

n <- 20
y <- rnorm(n, 0, 1)

For greater alternative: $H_A:F_Y\left(y\right)>\Phi (y;0,100)$ where $\Phi (y;\mu ,{\sigma }^2)$ is the c.d.f of the Normal$(\mu ,\sigma )$.

ks.test(y, pnorm, 0, 10, alternative = "greater")

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  y
## D^+ = 0.42016, p-value = 0.000513
## alternative hypothesis: the CDF of x lies above the null hypothesis

One sided tests are hard to interpret

For lower alternative: $H_A:F_Y\left(y\right)<\Phi (y;0,100)$:

ks.test(y, pnorm, 0, 10, alternative = "less")

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  y
## D^- = 0.44858, p-value = 0.0001717
## alternative hypothesis: the CDF of x lies below the null hypothesis

One sided tests

The combination of the two one-sided alternatives, does not cover all the possibilities for which the null hypothesis is false.

This makes it very hard to interpret one-sided KS tests - i.e. don’t do a one-sided test.

Estimating parameters

The KS test should only be used if you can completely specify $F_0$, the population distribution under the null hypothesis.

You should not estimate parameters from the data then do the test.

Kind of like trying to test $H_0:\mu =\overline{Y}$, you’ll rarely reject.

Next time…

After midterm: what if distribution is discrete?